Algorithms 之 sort & stable_sort
sort 应该是 <algorithm> 里面灰常喜闻乐见的东东了。 Sorting operations 除了 sort 和 stable_sort 这些之外,还有一些其他辅助设施。(以后 concept check 一律略)
先来热身的。is_sorted 和 is_sorted_until,后者是前者的一般化。
template<typename _ForwardIterator, typename _Compare>
_ForwardIterator
__is_sorted_until(_ForwardIterator __first, _ForwardIterator __last,
_Compare __comp)
{
if (__first == __last)
return __last;
_ForwardIterator __next = __first;
for (++__next; __next != __last; __first = __next, ++__next)
if (__comp(__next, __first))
return __next;
return __next;
}
is_sorted_until 的过程随便 yy 一下就能想到是怎样的,也没法优化。is_sorted_until 有一个稍微 tricky 的实现,用 adjacent_find。
std::adjacent_find(v1.begin(), v1.end(), std::greater<int>());
接下来正式进入 sort。std::sort 实现的是 quick sort 算法。先回忆一下 quick sort,就是每次选取一个 pivot,然后把小于和大于这个 pivot 的数据分别放在 pivot 两边,递归这个过程就可以得到有序的数组。而对于比较小的数组,采用插入排序会比直接快排快一点。
template<typename _RandomAccessIterator, typename _Compare>
inline void
__sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
_Compare __comp)
{
if (__first != __last)
{
std::__introsort_loop(__first, __last,
std::__lg(__last - __first) * 2,
__comp);
std::__final_insertion_sort(__first, __last, __comp);
}
}
看函数名猜功能,第一步做的应该是分 pivot,第二步应该是做划分之后的插入排序。
template<typename _RandomAccessIterator, typename _Size, typename _Compare>
void
__introsort_loop(_RandomAccessIterator __first,
_RandomAccessIterator __last,
_Size __depth_limit, _Compare __comp)
{
while (__last - __first > int(_S_threshold))
{
if (__depth_limit == 0)
{
std::__partial_sort(__first, __last, __last, __comp);
return;
}
--__depth_limit;
_RandomAccessIterator __cut =
std::__unguarded_partition_pivot(__first, __last, __comp);
std::__introsort_loop(__cut, __last, __depth_limit, __comp);
__last = __cut;
}
}
__introsort_loop 递归自己,直到 __first 和 __last 之间距离小于等于 _S_threshold。
enum { _S_threshold = 16 };
这个常数和插入排序,快速排序的实现以及机器本身的性质有关。
注意到还有一个 __depth_limit。如果它等于 0 之后就进行 __partial_sort。在外面调用的时候,__depth_limit 初始值为 std::__lg(__last - __first) * 2,也就是二分的深度。也就是说,如果选择 pivot 的时候太偏了,导致 __depth_limit 次 cut 后这部分长度还是大于 _S_threshold,就调用 __partial_sort 解决。
注意这里 __partial_sort 实际上已经对 __first 到 __last 做排序了。
template<typename _RandomAccessIterator, typename _Compare>
inline void
__partial_sort(_RandomAccessIterator __first,
_RandomAccessIterator __middle,
_RandomAccessIterator __last,
_Compare __comp)
{
std::__heap_select(__first, __middle, __last, __comp);
std::__sort_heap(__first, __middle, __comp);
}
看来 __partial_sort 实际上是堆排序。我来 yy 一下这里用堆排序的原因,堆排序的好处就是空间真的是 O(1) 的,快排实际上递归栈要有 O(lgN)。在前面 pick pivot 的过程中,期望是均分的,然而随机了 pick 这么多次都到不了,很可能就是数据本身的问题导致随机 pick pivot 效果不好,那么这时候快排相对不大合算,不如用 O(NlgN)复杂度的堆排序,省掉 O(lgN) 的空间。
__unguarded_partition_pivot 就是选择 pivot 的过程啦。
template<typename _RandomAccessIterator, typename _Compare>
inline _RandomAccessIterator
__unguarded_partition_pivot(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Compare __comp)
{
_RandomAccessIterator __mid = __first + (__last - __first) / 2;
std::__move_median_to_first(__first, __first + 1, __mid, __last - 1,
__comp);
return std::__unguarded_partition(__first + 1, __last, __first, __comp);
}
首先,__move_median_to_first 从 __first + 1,__mid,__last - 1 之间选择 median 放在 __first 位置。
template<typename _Iterator, typename _Compare>
void
__move_median_to_first(_Iterator __result,_Iterator __a, _Iterator __b,
_Iterator __c, _Compare __comp)
{
if (__comp(__a, __b))
{
if (__comp(__b, __c))
std::iter_swap(__result, __b);
else if (__comp(__a, __c))
std::iter_swap(__result, __c);
else
std::iter_swap(__result, __a);
}
else if (__comp(__a, __c))
std::iter_swap(__result, __a);
else if (__comp(__b, __c))
std::iter_swap(__result, __c);
else
std::iter_swap(__result, __b);
}
之后就是 partition 的过程了,把元素按 median 为分割分到左右两边。结束时 median 还是在之前的 __first 位置,这么做之后排序就多了一个元素,不过影响不大。
template<typename _RandomAccessIterator, typename _Compare>
_RandomAccessIterator
__unguarded_partition(_RandomAccessIterator __first,
_RandomAccessIterator __last,
_RandomAccessIterator __pivot, _Compare __comp)
{
while (true)
{
while (__comp(__first, __pivot))
++__first;
--__last;
while (__comp(__pivot, __last))
--__last;
if (!(__first < __last))
return __first;
std::iter_swap(__first, __last);
++__first;
}
}
做好划分之后,就到了最后的插入排序阶段。
template<typename _RandomAccessIterator, typename _Compare>
void
__final_insertion_sort(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Compare __comp)
{
if (__last - __first > int(_S_threshold))
{
std::__insertion_sort(__first, __first + int(_S_threshold), __comp);
std::__unguarded_insertion_sort(__first + int(_S_threshold), __last,
__comp);
}
else
std::__insertion_sort(__first, __last, __comp);
}
还是递归自己,在从开头到 _S_threshold 内做插入排序,对于剩下的部分做 __unguarded_insertion_sort。
template<typename _RandomAccessIterator, typename _Compare>
inline void
__unguarded_insertion_sort(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Compare __comp)
{
for (_RandomAccessIterator __i = __first; __i != __last; ++__i)
std::__unguarded_linear_insert(__i,
__gnu_cxx::__ops::__val_comp_iter(__comp));
}
template<typename _RandomAccessIterator, typename _Compare>
void
__unguarded_linear_insert(_RandomAccessIterator __last,
_Compare __comp)
{
typename iterator_traits<_RandomAccessIterator>::value_type
__val = _GLIBCXX_MOVE(*__last);
_RandomAccessIterator __next = __last;
--__next;
while (__comp(__val, __next))
{
*__last = _GLIBCXX_MOVE(*__next);
__last = __next;
--__next;
}
*__last = _GLIBCXX_MOVE(__val);
}
__unguarded_insertion_sort 顾名思义就是没有守卫的插入排序,每次从一个位置开始,向前搜索插入位置,不过前面没有指定停止的 guard。不过注意到之前是 __insertion_sort 过的,所以前面总是存在一个小于 *__last 的值作为搜索的终止点,使 __comp(__val, __next) == false。
那怎么证明这个过程的正确性呢?循环不变式(loop invariant)上次见已经不知道什么时候,实习面试的时候还被用这个教育了一下。在这里小试一下~~ 用循环不变式来证明关键是要先找到这个不变式。在这里,不变式是“以 __last 的为边界的左开区间中的元素总是大于 __val,而且保持原来的顺序;__next == __last - 1”。(假设 _comp 是小于)
- 循环初始化时,
__last右边没有元素(这里没必要考虑数组右边,因为操作都是都是向左),__next == __last - 1。 - 循环递推,满足
__val < *__next,则__next的元素被放到__last位置上,此时__last和__next分别向前移一位,__next == __last - 1。而__last的左开区间中都是之前移动到这里的元素,根据有序性是小于目前的__last的元素,所以有序性在递推时得到保持。 - 循环终止,由于前置的条件,之前总是存在一个点使
_comp结果为 false。终止时__last右边都是比__val大的有序元素。而__last这点正是__val需要插入的位置,*__next < __val。
正是因为这个性质,在做这个 __unguarded_insertion_sort 的时候,每次都是在之前的一个 partition (小于等于 _S_threshold )内插入,也就是说在一个 partition 内做插入排序。
而对于 __partial_sort 的部分,因为本身已经有序,实际上不会做插入排序,只是对每个位置多做了一次无用的判断而已。
其实还差一个 __insertion_sort 没有看,不过插入排序都很熟悉了。
template<typename _RandomAccessIterator, typename _Compare>
void
__insertion_sort(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Compare __comp)
{
if (__first == __last) return;
for (_RandomAccessIterator __i = __first + 1; __i != __last; ++__i)
{
if (__comp(__i, __first))
{
typename iterator_traits<_RandomAccessIterator>::value_type
__val = _GLIBCXX_MOVE(*__i);
_GLIBCXX_MOVE_BACKWARD3(__first, __i, __i + 1);
*__first = _GLIBCXX_MOVE(__val);
}
else
std::__unguarded_linear_insert(__i,
__gnu_cxx::__ops::__val_comp_iter(__comp));
}
}
也是利用 __unguarded_linear_insert 来做。在确定之前有一个 guard 之后,后面一律调 unguard 来做了。
除了 sort 呢,还有一个 stable_sort。stable_sort 保持了相等元素排序前后的顺序不变。冒泡排序、插入排序、归并排序这些都是稳定的,然而快排是万万不是的。
template<typename _RandomAccessIterator, typename _Compare>
inline void
__stable_sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
_Compare __comp)
{
typedef typename iterator_traits<_RandomAccessIterator>::value_type
_ValueType;
typedef typename iterator_traits<_RandomAccessIterator>::difference_type
_DistanceType;
typedef _Temporary_buffer<_RandomAccessIterator, _ValueType> _TmpBuf;
_TmpBuf __buf(__first, __last);
if (__buf.begin() == 0)
std::__inplace_stable_sort(__first, __last, __comp);
else
std::__stable_sort_adaptive(__first, __last, __buf.begin(),
_DistanceType(__buf.size()), __comp);
}
__stable_sort 里面申请了 __first 到 __last 长度的 buffer。如果 buffer 申请不到就转到 inplace 的 stable sort。
template<typename _RandomAccessIterator, typename _Compare>
void
__inplace_stable_sort(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Compare __comp)
{
if (__last - __first < 15)
{
std::__insertion_sort(__first, __last, __comp);
return;
}
_RandomAccessIterator __middle = __first + (__last - __first) / 2;
std::__inplace_stable_sort(__first, __middle, __comp);
std::__inplace_stable_sort(__middle, __last, __comp);
std::__merge_without_buffer(__first, __middle, __last,
__middle - __first,
__last - __middle,
__comp);
}
若元素小于等于 15 个,则直接去找插入排序。否则就分别对前半段和后半段递归,然后 inplace merge。也就是说,inplace 的本质就是小范围插入排序的 merge,利用 merge 降复杂度。那 inplace merge 是怎么做的呢?
template<typename _BidirectionalIterator, typename _Distance,
typename _Compare>
void
__merge_without_buffer(_BidirectionalIterator __first,
_BidirectionalIterator __middle,
_BidirectionalIterator __last,
_Distance __len1, _Distance __len2,
_Compare __comp)
{
if (__len1 == 0 || __len2 == 0)
return;
if (__len1 + __len2 == 2)
{
if (__comp(__middle, __first))
std::iter_swap(__first, __middle);
return;
}
先是对小值的特殊处理。
_BidirectionalIterator __first_cut = __first;
_BidirectionalIterator __second_cut = __middle;
_Distance __len11 = 0;
_Distance __len22 = 0;
if (__len1 > __len2)
{
__len11 = __len1 / 2;
std::advance(__first_cut, __len11);
__second_cut
= std::__lower_bound(__middle, __last, *__first_cut,
__gnu_cxx::__ops::__iter_comp_val(__comp));
__len22 = std::distance(__middle, __second_cut);
}
else
{
__len22 = __len2 / 2;
std::advance(__second_cut, __len22);
__first_cut
= std::__upper_bound(__first, __middle, *__second_cut,
__gnu_cxx::__ops::__val_comp_iter(__comp));
__len11 = std::distance(__first, __first_cut);
}
std::rotate(__first_cut, __middle, __second_cut);
_BidirectionalIterator __new_middle = __first_cut;
std::advance(__new_middle, std::distance(__middle, __second_cut));
std::__merge_without_buffer(__first, __first_cut, __new_middle,
__len11, __len22, __comp);
std::__merge_without_buffer(__new_middle, __second_cut, __last,
__len1 - __len11, __len2 - __len22, __comp);
}
__merge_without_buffer 做的事情可以用这张图来描述:
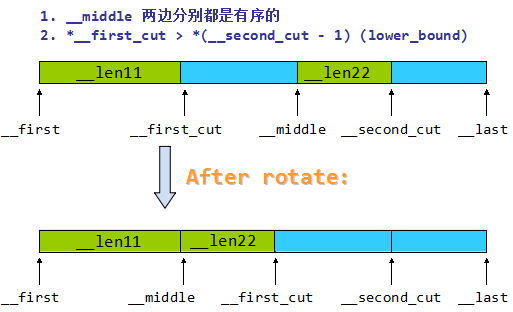
这样不断递归的做,最终将两段有序的部分合成一段有序的部分。来分析一下复杂度吧,std::rotate 是 O(n) (代码以后再说),平均情况下,的复杂度也就是 O(n) = 2 * O(n / 2) + O(n) / 2 ,还是 O(nlgn) 的复杂度。因为最后 15 以下会插入排序,所以前面会有一个“比较可观”的常数。
那如果有 buffer 可以用呢?情况就不至于这么惨,
template<typename _RandomAccessIterator, typename _Pointer,
typename _Distance, typename _Compare>
void
__stable_sort_adaptive(_RandomAccessIterator __first,
_RandomAccessIterator __last,
_Pointer __buffer, _Distance __buffer_size,
_Compare __comp)
{
const _Distance __len = (__last - __first + 1) / 2;
const _RandomAccessIterator __middle = __first + __len;
if (__len > __buffer_size)
{
std::__stable_sort_adaptive(__first, __middle, __buffer,
__buffer_size, __comp);
std::__stable_sort_adaptive(__middle, __last, __buffer,
__buffer_size, __comp);
}
else
{
std::__merge_sort_with_buffer(__first, __middle, __buffer, __comp);
std::__merge_sort_with_buffer(__middle, __last, __buffer, __comp);
}
std::__merge_adaptive(__first, __middle, __last,
_Distance(__middle - __first),
_Distance(__last - __middle),
__buffer, __buffer_size,
__comp);
}
如果 buffer 不够用的话这里也可以做到。关键在 __merge_sort_with_buffer 和 __merge_adaptive。
enum { _S_chunk_size = 7 };
template<typename _RandomAccessIterator, typename _Pointer, typename _Compare>
void
__merge_sort_with_buffer(_RandomAccessIterator __first,
_RandomAccessIterator __last,
_Pointer __buffer, _Compare __comp)
{
typedef typename iterator_traits<_RandomAccessIterator>::difference_type
_Distance;
const _Distance __len = __last - __first;
const _Pointer __buffer_last = __buffer + __len;
_Distance __step_size = _S_chunk_size;
std::__chunk_insertion_sort(__first, __last, __step_size, __comp);
while (__step_size < __len)
{
std::__merge_sort_loop(__first, __last, __buffer,
__step_size, __comp);
__step_size *= 2;
std::__merge_sort_loop(__buffer, __buffer_last, __first,
__step_size, __comp);
__step_size *= 2;
}
}
看来又把插入排序拿出来了。
template<typename _RandomAccessIterator, typename _Distance,
typename _Compare>
void
__chunk_insertion_sort(_RandomAccessIterator __first,
_RandomAccessIterator __last,
_Distance __chunk_size, _Compare __comp)
{
while (__last - __first >= __chunk_size)
{
std::__insertion_sort(__first, __first + __chunk_size, __comp);
__first += __chunk_size;
}
std::__insertion_sort(__first, __last, __comp);
}
__chunk_insertion_sort 做的事情就是按 _S_chunk_size 为界,将 __first 和 __last 之间分成若干份,对于每一份做插入排序。
在之前的 while 循环里面,调用了两次 __merge_sort_loop,为了最后总是把元素归回原位,避免利用 merge 次奇偶判断元素是不是在 buffer 里。
template<typename _RandomAccessIterator1, typename _RandomAccessIterator2,
typename _Distance, typename _Compare>
void
__merge_sort_loop(_RandomAccessIterator1 __first,
_RandomAccessIterator1 __last,
_RandomAccessIterator2 __result, _Distance __step_size,
_Compare __comp)
{
const _Distance __two_step = 2 * __step_size;
while (__last - __first >= __two_step)
{
__result = std::__move_merge(__first, __first + __step_size,
__first + __step_size,
__first + __two_step,
__result, __comp);
__first += __two_step;
}
__step_size = std::min(_Distance(__last - __first), __step_size);
std::__move_merge(__first, __first + __step_size,
__first + __step_size, __last, __result, __comp);
}
__merge_sort_with_buffer 中每次将 step 乘 2,调用 __merge_sort_loop ,而 __merge_sort_loop 则是从 __first 到 __last,每 step * 2 个区域中做一次 merge。
真正做 merge 的是 __move_merge。
template<typename _InputIterator, typename _OutputIterator,
typename _Compare>
__move_merge(_InputIterator __first1, _InputIterator __last1,
_InputIterator __first2, _InputIterator __last2,
_OutputIterator __result, _Compare __comp)
{
while (__first1 != __last1 && __first2 != __last2)
{
if (__comp(__first2, __first1))
{
*__result = _GLIBCXX_MOVE(*__first2);
++__first2;
}
else
{
*__result = _GLIBCXX_MOVE(*__first1);
++__first1;
}
++__result;
}
return _GLIBCXX_MOVE3(__first2, __last2,
_GLIBCXX_MOVE3(__first1, __last1,
__result));
}
其实逻辑也蛮简单的~。
总结一下~~
- 复习了各种排序~ 排序的稳定性傻傻的。
- sort 的各种优化,小范围用插入,分布不均用堆排。
- inplace merge sort 的方法。
- 这里 sort 的几个过程用函数封装的很赞啊,不是一坨非常清晰。
- 小小复习一下循环不变式。
- 由于其他几个 sort 相关操作都跟 heap 的联系太紧密了,下次先把 heap 做了再说。